 05-栈、队列、优先队列
05-栈、队列、优先队列
# 栈的基础应用(有效的括号)
# 问题分析
20. 有效的括号 (opens new window)简单
给定一个只包括
'(',')','{','}','[',']'的字符串s,判断字符串是否有效。有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
遍历字符,如果遇到左括号就推入栈中,如果遇到右括号就取出栈顶的元素,看是不是匹配的左括号。
/**
* 栈解法
* 时间复杂度: O(n)
* 空间复杂度: O(n+∣Σ∣),其中 Σ 表示字符集,本题中字符串只包含 6 种括号,∣Σ∣=6
*/
class Solution {
public boolean isValid(String s) {
if ((s.length() % 2) != 0) {
return false;
}
Map<Character, Character> pairs = new HashMap<Character, Character>() {{
put(')', '(');
put('}', '{');
put(']', '[');
}};
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
if (pairs.containsKey(s.charAt(i))) {
if (stack.isEmpty() || stack.pop() != pairs.get(s.charAt(i)))
return false;
} else {
stack.push(s.charAt(i));
}
}
return stack.isEmpty();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 相关问题
150. 逆波兰表达式求值 (opens new window)中等
根据 逆波兰表示法 (opens new window),求表达式的值。
有效的算符包括
+、-、*、/。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:
- 整数除法只保留整数部分。
- 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
/**
* 栈解法
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack();
int num1, num2;
for (String token : tokens) {
switch (token) {
case "+":
stack.push((stack.pop() + stack.pop()));
break;
case "-":
num2 = stack.pop();
num1 = stack.pop();
stack.push((num1 - num2));
break;
case "*":
stack.push((stack.pop() * stack.pop()));
break;
case "/":
num2 = stack.pop();
num1 = stack.pop();
stack.push((num1 / num2));
break;
default:
stack.push(Integer.valueOf(token));
}
}
return stack.pop();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
给你一个字符串
path,表示指向某一文件或目录的 Unix 风格 绝对路径 (以'/'开头),请你将其转化为更加简洁的规范路径。在 Unix 风格的文件系统中,一个点(
.)表示当前目录本身;此外,两个点 (..) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠(即,'//')都被视为单个斜杠'/'。 对于此问题,任何其他格式的点(例如,'...')均被视为文件/目录名称。请注意,返回的 规范路径 必须遵循下述格式:
- 始终以斜杠
'/'开头。- 两个目录名之间必须只有一个斜杠
'/'。- 最后一个目录名(如果存在)不能 以
'/'结尾。- 此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含
'.'或'..')。返回简化后得到的 规范路径 。
/**
* 双端队列
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public String simplifyPath(String path) {
// 分割路径
String[] arr = path.split("/");
Deque<String> deque = new LinkedList<>();
// 有效路径入队列
for (String item : arr) {
switch (item) {
case "":
break;
case ".":
break;
case "..":
if (!deque.isEmpty()) {
deque.removeLast();
}
break;
default:
deque.addLast(item);
}
}
// 出队列拼接路径
StringBuilder sb = new StringBuilder();
while (!deque.isEmpty()) {
sb.append("/").append(deque.pop());
}
return sb.length() == 0 ? "/" : sb.toString();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 栈和递归的紧密关系(二叉树的前中后序遍历)
栈除了可以解决前面介绍的经典算法问题,栈其实还和递归有着极其紧密的关系。通常我们写一个递归算法是不会使用到栈的,但是理解栈和递归的关系,对于我们加深对递归的理解很有帮助。同时从操作系统的角度看,实现递归的方式正是使用栈。
# 问题分析
我们通过二叉树来看栈和递归的关系,用到的题目是二叉树的前中后序遍历。如果使用递归算法是非常简单的,这里我们讨论非递归实现,即使用栈。其实递归实现是有一个隐式的系统栈,迭代法需要我们显示的声明栈,两种方法的时间复杂度和空间复杂度都是 O(n) 的。
/**
* 二叉树前中后序遍历通用模板
*/
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack<>();
while (root != null || !stack.isEmpty()) { // 统一的循环条件
// (1) 左链入栈
while (root != null) {
stack.push(root);
root = root.left;
}
// (2) 出栈一个
root = stack.pop();
// (3) root 变换
root = xxx;
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
如上述模板,对于前中后序遍历,我们只需要考虑遍历元素的时机即可,即 res.add(root.val) 的时机。
前序遍历是在入栈前加入,中序遍历是在入栈后加入,其余代码一模一样。
后序遍历涉及到重入栈操作,所以对于出栈元素有两种情况:
- 当出栈节点的右孩子为空或右孩子已经遍历到时,执行
res.add(root.val),并变换root = null; - 否则需要先遍历右孩子,重入栈
stack.push(root),并变换root = root.right。
因为需要期间需要判断出栈节点的右孩子是否被遍历过,所以需要维护一个指针
prev指向上一个被遍历到的节点,初始为 null。- 当出栈节点的右孩子为空或右孩子已经遍历到时,执行
# 代码实现
使用上述总结的代码模板,就可以很轻松的写出前中后序遍历的非递归实现了,但一定要通过 leetcode 解析加以理解。这里只给出非递归实现,递归实现很简单,略。
144. 二叉树的前序遍历 (opens new window)简单
给你二叉树的根节点
root,返回它节点值的 前序 遍历。
/**
* 迭代法,栈
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack<>();
while (root != null || !stack.isEmpty()) { // 统一的循环条件
// (1) 左链入栈
while (root != null) {
res.add(root.val); // 遍历访问时机
stack.push(root);
root = root.left;
}
// (2) 出栈一个
root = stack.pop();
// (3) root 变换
root = root.right;
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
94. 二叉树的中序遍历 (opens new window)简单
给定一个二叉树的根节点
root,返回它的 中序 遍历。
/**
* 迭代法,栈
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack<>();
while (root != null || !stack.isEmpty()) { // 统一的循环条件
// (1) 左链入栈
while (root != null) {
stack.push(root);
root = root.left;
}
// (2) 出栈一个
root = stack.pop();
res.add(root.val); // 遍历访问时机
// (3) root 变换
root = root.right;
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
145. 二叉树的后序遍历 (opens new window)简单
给定一个二叉树,返回它的 后序 遍历。
/**
* 迭代法,栈
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack<>();
TreeNode prev = null; // 涉及到重入栈,需维护上一个遍历的节点
while (root != null || !stack.isEmpty()) { // 统一的循环条件
// (1) 左链入栈
while (root != null) {
stack.push(root);
root = root.left;
}
// (2) 出栈一个
root = stack.pop();
if (root.right == null || root.right == prev) {
prev = root;
res.add(root.val); // 遍历访问时机
root = null; // (3) root 变换
} else {
stack.push(root);
root = root.right; // (3) root 变换
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 相关问题
341. 扁平化嵌套列表迭代器 (opens new window)中等
给你一个嵌套的整数列表
nestedList。每个元素要么是一个整数,要么是一个列表;该列表的元素也可能是整数或者是其他列表。请你实现一个迭代器将其扁平化,使之能够遍历这个列表中的所有整数。实现扁平迭代器类
NestedIterator:
NestedIterator(List nestedList)用嵌套列表nestedList初始化迭代器。int next()返回嵌套列表的下一个整数。boolean hasNext()如果仍然存在待迭代的整数,返回true;否则,返回false。你的代码将会用下述伪代码检测:
initialize iterator with nestedList res = [] while iterator.hasNext() append iterator.next() to the end of res return res1
2
3
4
5如果
res与预期的扁平化列表匹配,那么你的代码将会被判为正确。
/**
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
public class NestedIterator implements Iterator<Integer> {
private LinkedList<Integer> data;
public NestedIterator(List<NestedInteger> nestedList) {
data = new LinkedList<>();
this.dfs(nestedList);
}
private void dfs(List<NestedInteger> nestedList) {
for (NestedInteger item : nestedList) {
if (item.isInteger()) {
data.add(item.getInteger());
} else {
dfs(item.getList());
}
}
}
@Override
public Integer next() {
return data.pop();
}
@Override
public boolean hasNext() {
return !data.isEmpty();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 队列的典型应用(二叉树的层序遍历)
# 问题分析
这一节我们来看队列这种数据结构能够处理什么算法问题。对队列来说,它主要处理的算法问题是 广度优先遍历 。提到广度优先遍历,大多数时候是针对图的,其实对于树和图都有广度优先遍历,在树和图中广度优先遍历可以解决以下问题。
- 树:层序遍历
- 图:无权图的最短路径
102. 二叉树的层序遍历 (opens new window)中等
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
但是在二叉树层序遍历的过程中,不能仅仅用广度优先遍历,因为本题要求返回的是每一层的节点值,即要将节点属于那一层区分开,所以要变化一下,每次循环内再开个循环,内循环处理完当前层的节点。但是两层循环并没有增多节点访问次数,只是一种“分批”处理的方式,详细可参考:BFS 的使用场景总结:层序遍历、最短路径问题 (opens new window)。
/**
* 广度优先遍历
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> level = new ArrayList<>(); // 存放当前层节点
int currentLevelSize = queue.size(); // 当前层节点数
for (int i = 0; i < currentLevelSize; i++) { // 内循环处理完当前层节点
TreeNode node = queue.poll();
level.add(node.val);
if (node.left != null)
queue.offer(node.left);
if (node.right != null)
queue.offer(node.right);
}
res.add(level);
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 相关问题
107. 二叉树的层序遍历 II (opens new window)中等
给定一个二叉树,返回其节点值自底向上的层序遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
例如: 给定二叉树
[3,9,20,null,null,15,7],3 / \ 9 20 / \ 15 71
2
3
4
5返回其自底向上的层序遍历为:
[ [15,7], [9,20], [3] ]1
2
3
4
5
/**
* 广度优先遍历
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> res = new LinkedList<>();
if (root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> list = new ArrayList<>();
int size = queue.size(); // 一次遍历一层
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
list.add(node.val);
if (node.left != null)
queue.offer(node.left);
if (node.right != null)
queue.offer(node.right);
}
res.add(0, list); // 头插
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
103. 二叉树的锯齿形层序遍历 (opens new window)中等
给定一个二叉树,返回其节点值的锯齿形层序遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如: 给定二叉树
[3,9,20,null,null,15,7],3 / \ 9 20 / \ 15 71
2
3
4
5返回锯齿形层序遍历如下:
[ [3], [20,9], [15,7] ]1
2
3
4
5
/**
* 广度优先遍历
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
boolean isOrderLeft = true; // true: 正序; false: 逆序
while (!queue.isEmpty()) {
List<Integer> list = new ArrayList<>();
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
list.add(isOrderLeft ? list.size() : 0, node.val);
if (node.left != null)
queue.offer(node.left);
if (node.right != null)
queue.offer(node.right);
}
res.add(list);
isOrderLeft = !isOrderLeft;
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
199. 二叉树的右视图 (opens new window)中等
给定一个二叉树的 根节点
root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
/**
* 广度优先遍历
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size(); // 本层节点数
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
if (node.left != null)
queue.offer(node.left);
if (node.right != null)
queue.offer(node.right);
if (i == size - 1) // 本层最后一个
res.add(node.val);
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# BFS 和图的最短路径(完全平方数)
# 题目分析
广度优先遍历除了解决树的层序遍历外,还可以处理图的最短路径问题,关于求图的最短路径算法这里不做讨论。这里介绍很多算法问题使用图的最短路径算法思路来解决,但是这些问题看上去却不像是一个图论的问题,题目并没有告诉我们这是个关于图论的问题,这时候需要我们对问题深入分析,进行建模。
279. 完全平方数 (opens new window)中等
给定正整数 n,找到若干个完全平方数(比如
1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。给你一个整数
n,返回和为n的完全平方数的 最少数量 。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,
1、4、9和16都是完全平方数,而3和11不是。
直觉可能会让我们使用贪心算法尽量填入数值大的完全平方数来解决这个问题,这是不成立的。以 12 为例,如果使用贪心算法将得到 12=9+1+1+1,为 4 个完全平方数的和,但正确答案是 3 个,12=4+4+4。
**对问题建模:**整个问题转化为一个图论问题。从 n 到 0,每个数字表示一个节点,如果两个数字 x 和 y 差值是一个完全平方数,则连接一条边。这样得到一个无权图,原问题转化成,求这个无权图中从 n 到 0 的最短路径。
以 n=6 为例,用上述思路建立下图,每个相连接的节点之间的差值都是一个完全平方数,这里建立的是有向图,由大的节点指向小的节点,我们可以搜索从 n 到 0 的最短路径就是问题的解,即从 n 减去多少个完全平方数到 0。
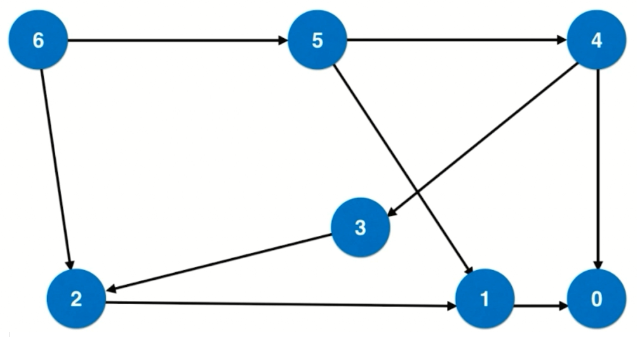
对上述图进行广度优先遍历,过程如下:
- 起点 6 入队列,再拿出来,考察 6 指向的所有节点,即 6 减去一个小于 6 个完全平方数
BFS 基础实现:
/**
* 用图论的 BFS
* 时间复杂度: O(2^n)
* 空间复杂度: O(2^n)
*/
class Solution {
public int numSquares(int n) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(n);
int step = 0; // 经过几步到当前层级
while (!queue.isEmpty()) {
int currentBreadthSize = queue.size(); // 当前层级的节点数
for (int i = 0; i < currentBreadthSize; i++) { // 遍历当前层级的节点
Integer num = queue.poll();
// 当前层级出现 0 节点,说明可达了,返回经过步数 step
if (num == 0) return step;
// 如果不是 0 节点,将该节点的下一层级节点入队列(但不不在本轮遍历,下一轮才到它们)
for (int j = 1; num - j * j >= 0; j++) { // 下一层级是本节点减去一个完全平方数
queue.offer(num - j * j);
}
}
step++; // 一个层级的遍历完了,step+1 进入下一层级
}
throw new IllegalStateException("No Solution.");
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
BFS 优化一:
可以试验下对于 n 比较小的情况这个程序可以比较好的完成任务,但是这个程序其实并非一个标准的广度优先实现,这段代码是有性能问题的,因为我们每次都将节点 num 减去一个完全平方数的结果推入了队列,这里我们重复推入了很多节点,是因为对于每一个数字来说我们可以从多种渠道来获得,比如 1 这个节点,2-1 和 5-4 等等都能得到 1,因为我们现在的结构是一个图,每个节点可以有多个节点指向它,所以我们这种代码实现会将冗余的节点推入队列,其实只需要第一次访问到才入队就好了,后面再遇到经过的路程肯定比这条路长了。
为了解决这个问题,我们需要记录哪些节点已经入过队列了,代码如下。
/**
* 用图论的 BFS 改进
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution2 {
public int numSquares(int n) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(n);
// 记录节点是否被访问过,visited[i] == true 表示节点 i 入过队列
boolean[] visited = new boolean[n + 1];
visited[n] = true;
int step = 0; // 经过几步到当前层级
while (!queue.isEmpty()) {
int currentBreadthSize = queue.size(); // 当前层级的节点数
for (int i = 0; i < currentBreadthSize; i++) { // 遍历当前层级的节点
Integer num = queue.poll();
if (num == 0) return step; // 当前层级出现 0 节点,说明可达了,返回经过步数 step
// 如果不是 0 节点,将该节点的下一层级节点入队列(但不不在本轮遍历,下一轮才到它们)
for (int j = 1; num - j * j >= 0; j++) {
int next = num - j * j;
// 如果访问过,说明之前的层就已经访问过了,所以比这条路短,没必要入队
if (!visited[next]) {
queue.offer(next);
visited[next] = true;
}
}
}
step++; // 一个层级的遍历完了,step+1 进入下一层级
}
throw new IllegalStateException("No Solution.");
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
BFS 优化二:
上述代码还可以进一步优化,下一层级节点入队前判断是否是重点,如果是直接返回 step + 1 即可,避免了再向下遍历一层广度。经过此简单优化,leetcode 时间消耗从 27ms 加快到 7ms。
/**
* 用图论的 BFS 改进,下一节点入队前判断是否是重点
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public int numSquares(int n) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(n);
// 记录节点是否被访问过,visited[i] == true 表示节点 i 入过队列
boolean[] visited = new boolean[n + 1];
visited[n] = true;
int step = 0; // 经过几步到当前层级
while (!queue.isEmpty()) {
int currentBreadthSize = queue.size(); // 当前层级的节点数
for (int i = 0; i < currentBreadthSize; i++) { // 遍历当前层级的节点
Integer num = queue.poll();
if (num == 0) return step; // 当前层级出现 0 节点,说明可达了,返回经过步数 step
// 如果不是 0 节点,将该节点的下一层级节点入队列(但不不在本轮遍历,下一轮才到它们)
for (int j = 1; num - j * j >= 0; j++) {
int next = num - j * j;
if (next == 0)
return step + 1; // 入队前判断下一节点是否为 0,如果是说明再走一步就到了
// 如果访问过,说明之前的层就已经访问过了,所以比这条路短,没必要入队
if (!visited[next]) {
queue.offer(next);
visited[next] = true;
}
}
}
step++; // 一个层级的遍历完了,step+1 进入下一层级
}
throw new IllegalStateException("No Solution.");
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
至此,我们将这个看上去和图论无关的问题通过建模,转化为图论问题,进而使用广度优先遍历种的最短路径思想得到了问题的答案。
附:动态规划解法
更容易想到的方法,但经过 leetcode 测试效率不如 BFS 。
/**
* 动态规划
* 时间复杂度: O(n^2)
* 空间复杂度: O(n)
*/
class Solution {
public int numSquares(int n) {
int[] f = new int[n + 1];
for (int i = 1; i <= n; i++) {
int min = Integer.MAX_VALUE;
for (int j = 1; j * j <= i; j++) {
min = Math.min(min, 1 + f[n - j * j]);
}
f[i] = min;
}
return f[n];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 相关问题
下面两个问题都是广度优先遍历相关的。
127. 单词接龙 (opens new window)困难
字典
wordList中从单词beginWord和endWord的 转换序列 是一个按下述规格形成的序列:
- 序列中第一个单词是
beginWord。- 序列中最后一个单词是
endWord。- 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典
wordList中的单词。给你两个单词
beginWord和endWord和一个字典wordList,找到从beginWord到endWord的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
/**
* 广度优先遍历
*/
class Solution {
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
if (!wordList.contains(endWord))
return 0;
Queue<String> queue = new LinkedList<>(); // 队列用于 BFS
queue.offer(beginWord);
HashSet<String> visited = new HashSet<>(); // 用于记录已经访问过的节点
visited.add(beginWord);
int count = 1; // BFS 经过的层数
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
String preWord = queue.poll(); // 前一层的单词
// 如果可以转换为 endWord,直接返回
if (canConvert(preWord, endWord))
return count + 1;
// 遍历 wordList,找到能转换的单词,入队
for (String item : wordList) {
// 未访问过且能转换,入队并记录访问状态
if (!visited.contains(item) && canConvert(preWord, item)) {
queue.offer(item);
visited.add(item);
}
}
}
count++;
}
return 0;
}
// 判断是否能转换
private boolean canConvert(String str1, String str2) {
int def = 0;
for (int i = 0; i < str1.length(); i++) {
if (str1.charAt(i) != str2.charAt(i))
def++;
if (def > 1)
return false;
}
return true;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
126. 单词接龙 II (opens new window)困难
按字典
wordList完成从单词beginWord到单词endWord转化,一个表示此过程的 转换序列 是形式上像beginWord -> s1 -> s2 -> ... -> sk这样的单词序列,并满足:
- 每对相邻的单词之间仅有单个字母不同。
- 转换过程中的每个单词
si(1 <= i <= k)必须是字典wordList中的单词。注意,beginWord不必是字典wordList中的单词。sk == endWord给你两个单词
beginWord和endWord,以及一个字典wordList。请你找出并返回所有从beginWord到endWord的 最短转换序列 ,如果不存在这样的转换序列,返回一个空列表。每个序列都应该以单词列表[beginWord, s1, s2, ..., sk]的形式返回。
# 优先队列相关的算法问题(前 K 个高频元素)
# 题目分析
通常来说优先队列的底层实现是使用堆,对于堆的实现,希望能达到白板编程的水平。
347. 前 K 个高频元素 (opens new window)中等
给你一个整数数组
nums和一个整数k,请你返回其中出现频率前k高的元素。你可以按 任意顺序 返回答案。
使用容量为 k 的最小堆实现。
/**
* 最小堆实现
* 时间复杂度: O(Nlogk),堆的操作 logk
* 空间复杂度: O(N)
*/
class Solution {
public int[] topKFrequent(int[] nums, int k) {
// 统计每个元素出现的次数,key-元素,value-元素出现的次数
HashMap<Integer, Integer> map = new HashMap<>();
for (int item : nums)
map.put(item, map.getOrDefault(item, 0) + 1);
// 遍历 map,用最小堆保存频率最大的 k 个元素
PriorityQueue<Integer> queue = new PriorityQueue<>((o1, o2) -> map.get(o1) - map.get(o2));
for (Integer key : map.keySet()) {
if (queue.size() < k) {
queue.offer(key);
} else if (map.get(key) > map.get(queue.peek())) {
queue.poll();
queue.offer(key);
}
}
// 取出最小堆中的元素
int[] res = new int[k];
for (int i = 0; i < k; i++)
res[i] = queue.poll();
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 相关问题
23. 合并K个升序链表 (opens new window)困难
给你一个链表数组,每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中,返回合并后的链表。
k 个一组对比
/** * k 个一组对比,暴力解 * 力扣耗时 1015 ms */ class Solution1 { public ListNode mergeKLists(ListNode[] lists) { int k = lists.length; ListNode dummyHead = new ListNode(-1); ListNode pre = dummyHead; HashSet<Integer> finished = new HashSet<>(); while (finished.size() < k) { int index = -1; for (int i = 0; i < k; i++) { if (lists[i] == null) finished.add(i); else if (index == -1 || lists[i].val < lists[index].val) index = i; } if (index != -1) { ListNode node = lists[index]; lists[index] = node.next; node.next = null; pre.next = node; pre = pre.next; } } return dummyHead.next; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29两两合并
/** * 两两归并 * 时间复杂度: O(k^2 * n), 力扣耗时 100 ms * 空间复杂度: O(1) */ class Solution2 { public ListNode mergeKLists(ListNode[] lists) { ListNode res = null; for (ListNode list : lists) { res = mergeTwoLists(res, list); } return res; } // 合并两个链表 private ListNode mergeTwoLists(ListNode l1, ListNode l2) { if (l1 == null || l2 == null) return l1 == null ? l2 : l1; ListNode dummyHead = new ListNode(-1); ListNode pre = dummyHead; while (l1 != null && l2 != null) { if (l1.val < l2.val) { pre.next = l1; l1 = l1.next; } else { pre.next = l2; l2 = l2.next; } pre = pre.next; } pre.next = l1 == null ? l2 : l1; return dummyHead.next; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34分治合并
/** * 分治归并 * 时间复杂度: O(kn * logk), 力扣耗时 1 ms * 空间复杂度: O(logk) */ class Solution3 { public ListNode mergeKLists(ListNode[] lists) { return merge(lists, 0, lists.length - 1); } // 二分合并 private ListNode merge(ListNode[] lists, int l, int r) { if (l == r) return lists[l]; if (l > r) return null; int mid = (l + r) >> 1; ListNode l1 = merge(lists, l, mid); ListNode l2 = merge(lists, mid + 1, r); return mergeTwoLists(l1, l2); } // 合并两个链表 private ListNode mergeTwoLists(ListNode l1, ListNode l2) { if (l1 == null || l2 == null) return l1 == null ? l2 : l1; ListNode dummyHead = new ListNode(-1); ListNode pre = dummyHead; while (l1 != null && l2 != null) { if (l1.val < l2.val) { pre.next = l1; l1 = l1.next; } else { pre.next = l2; l2 = l2.next; } pre = pre.next; } pre.next = l1 == null ? l2 : l1; return dummyHead.next; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40优先级队列
/** * 使用优先级队列 * 时间复杂度: O(kn * logk), 力扣耗时 6 ms * 空间复杂度: O(k) */ class Solution4 { public ListNode mergeKLists(ListNode[] lists) { PriorityQueue<ListNode> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o.val)); for (ListNode list : lists) { if (list != null) queue.offer(list); } ListNode dummyHead = new ListNode(-1); ListNode tail = dummyHead; while (!queue.isEmpty()) { ListNode node = queue.poll(); if (node.next != null) { queue.offer(node.next); node.next = null; } tail.next = node; tail = tail.next; } return dummyHead.next; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
