CodeAshen's blog
CodeAshen
2023-02-10
目录

02-数组问题

# 第一个有关的数组算法（移动零）

# 问题描述

283. 移动零 (opens new window)简单

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

例：输入: [0,1,0,3,12]，输出: [1,3,12,0,0]

# 分析实现

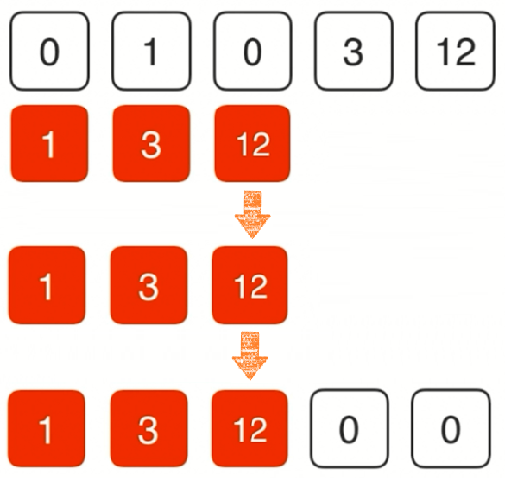
  1. 方法一：使用辅助空间 list 存储数组中的非零元素，先扫描数组将非零元素放到 list 中，然后将 list 中元素依次从前往后放回数组中，最后数组为填充到的后面部分填零。

    image-20210829092031834

    /**
 * 借助 List 存放非 0 元素
 * 时间复杂度: O(n)
 * 空间复杂度: O(n)
 */
class solution {
    public void moveZeroes(int[] nums) {
        List<Integer> nonZeroElements = new ArrayList<>();

        // 将 vec 中所有非 0 元素放入 nonZeroElements中
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) {
                nonZeroElements.add(nums[i]);
            }
        }

        // 将 nonZeroElements 中的所有元素依次放入到 nums 开始的位置
        for (int i = 0; i < nonZeroElements.size(); i++) {
            nums[i] = nonZeroElements.get(i);
        }

        // 将 nums 剩余的位置放置为 0
        for (int i = nonZeroElements.size(); i < nums.length; i++) {
            nums[i] = 0;
        }
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
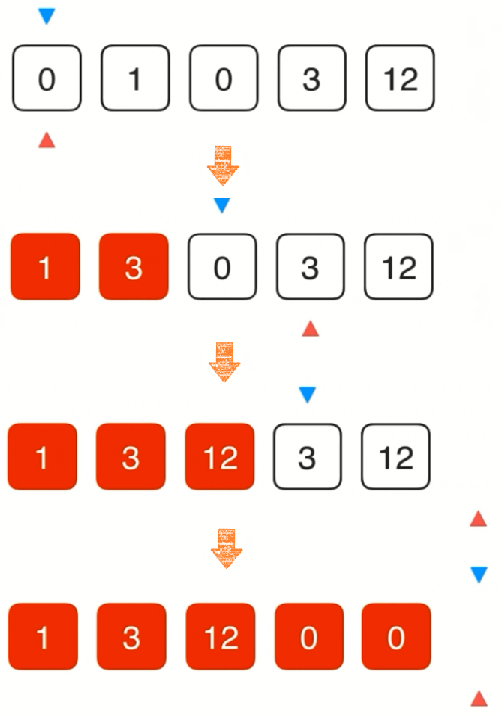
    27

  2. 方法二：不使用辅助空间，扫描数组过程中，将非零元素移到数组前面。过程中维护索引 k，[0...k) 中保存所有当前遍历过的非零元素。

    image-20210829091903379

    /**
 * 不借助辅助空间，原地排序
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class solution {
    public void moveZeroes(int[] nums) {
        // 标识临界索引
        int k = 0;

        // 第一次完全遍历，将非 0 元素填充到前面，同时维护 k
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) {
                nums[k] = nums[i];
                k++;
            }
        }
        // 从 k 开始遍历，填充 0
        for (int i = k; i < nums.length; i++) {
            nums[i] = 0;
        }
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23

  3. 方法三：通过交换省略填充零的操作，避免第二次扫描。[0...k) 中保存所有当前遍历过的非零元素，换言之 k 指向第一个 0 元素，扫描到元素 i 时，逢 0 跳过，非 0 则交换 k 和 i 位置元素，然后向后移一位。

    /**
 * 通过交换，不需要最后的填充 0 操作
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class solution {
    public void moveZeroes(int[] nums) {
        // k 指向当前第一个 0 元素
        int k = 0;
        // 完全遍历，如果遇到非 0 元素，和 k 指向的 0 元素交换，k++
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) {
                swap(nums, i, k);
                k++;
            }
        }
    }

    private void swap(int[] nums, int i, int j) {
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24

  4. 方法四：在方法三的基础上改进，避免一直没遇到 0 元素，k 和 i 指向同一元素，自己和自己交换的操作。

    /**
 * 在 solution3 的基础上避免了如果没有遇到 0 元素，k 和 i 同步前进，需要自己和自己交换的操作
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class solution {
    public void moveZeroes(int[] nums) {
        int k = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) {
                if (k != i) {   // k、i 不相等才交换
                    swap(nums, i, k);
                }
                k++;
            }
        }
    }

	// 省略 swap 方法
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20

# 相关问题

27. 移除元素 (opens new window)简单

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

/**
 * 双指针
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    public int removeElement(int[] nums, int val) {
        int k = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != val) {
                nums[k] = nums[i];
                k++;
            }
        }
        return k;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

26. 删除有序数组中的重复项 (opens new window)简单

给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

/**
 * 双指针
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    public int removeDuplicates(int[] nums) {
        if (nums.length == 0) 
            return 0;

        // 指针含义: 元素个数; 不重复序列的下一索引
        int k = 1;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] != nums[k - 1]) {
                nums[k] = nums[i];
                k++;
            }
        }
        return k;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

80. 删除有序数组中的重复项 II (opens new window)中等

给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使每个元素 最多出现两次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

/**
 * 双指针
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    public int removeDuplicates(int[] nums) {
        int n = nums.length;
        if (n <= 2) return n;
        
        // 指针含义：符合条件的数组下一个指针；即符合条件的数组长度
        int k = 2;
        for (int i = 2; i < n; i++) {
            if (nums[i] != nums[k - 1] || nums[k - 1] != nums[k - 2]) {
                nums[k] = nums[i];
                k++;
            }
        }
        return k;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 三路快排 partition 思路的应用（颜色分类）

# 问题描述

75. 颜色分类 (opens new window)中等

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]
1
2

本题其实直接对数组排序就能完成操作，如使用快速排序，时间复杂度是 O(nlogn)，当然题目显然不是让我们直接调用函数库中的排序操作。

# 分析实现

  1. 计数排序：因为数组中只有 0、1、2，我们可以扫描一遍数组，统计三个数的频次，然后依次填充回数组即可。这就是计数排序，适用于元素个数非常少的情况。

    /**
 * 计数排序的思路, 对整个数组遍历了两遍
 * 时间复杂度: O(n)
 * 空间复杂度: O(k), k 为元素的取值范围, 可以视为 O(1)
 */
class Solution {
    public void sortColors(int[] nums) {
        int[] count = {0, 0, 0};  // 分别统计 0, 1, 2 
        for (int i = 0; i < nums.length; i++) {
            count[nums[i]]++;
        }

        int index = 0;
        for (int i = 0; i < count[0]; i++) {
            nums[index++] = 0;
        }
        for (int i = 0; i < count[1]; i++) {
            nums[index++] = 1;
        }
        for (int i = 0; i < count[2]; i++) {
            nums[index++] = 2;
        }
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24

    这里我们扫描了数组两边，第一遍统计元素个数，第二遍填充元素。我们有没有可能只扫描数组一遍就解决问题呢？

  2. 三路快排 partition 操作：借助三路快排中 partition 操作的思路，扫描数组的过程中交换元素并维护两个索引位，就能将只有三个元素的数组排好序。

    image-20210829103622342

    /**
 * 三路快速排序的思想, 对整个数组只遍历了一遍
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    public void sortColors(int[] nums) {
        int zero = -1;          // [0...zero] == 0
        int two = nums.length;  // [two...n-1] == 2
        for (int i = 0; i < two; ) {
            if (nums[i] == 1) {
                i++;
            } else if (nums[i] == 0) {
                swap(nums, i, zero + 1);
                zero++;
                i++;
            } else {  // nums[i] == 2
                swap(nums, i,  two - 1);
                two--;
                // 这种情况索引 i 不变
            }
        }
    }

    // 省略 swap 方法
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26

# 相关问题

88. 合并两个有序数组 (opens new window)简单

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

/**
 * 三指针归并
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    // 将 nums2 归并入 nums1，若从左往右归并会丢失 num1 的左侧待归并元素，
    // nums1 右侧有剩余，应该从右往左归并
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        // 两待归并部分的右边界指针
        int i = m - 1, j = n - 1;
        
        // 开始从右往左归并
        for (int k = (n + m - 1); k >= 0; k--) {
            // 如果 nums1 归并完了，nums2 依次并入 nums1 即可
            if (i < 0) {
                nums1[k] = nums2[j--];
                continue;
            }
            // 如果 nums2 归并完了，nums1 就在对应位置，无需继续归并
            if (j < 0) break;
            
            // 取出两部分较小者并入，并维护索引值
            nums1[k] = nums1[i] > nums2[j] ? 
                    nums1[i--] : nums2[j--];
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

215. 数组中的第K个最大元素 (opens new window)中等

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

这题只要使用排序就可以得到结果，时间复杂度是 O(nlogn)，其实可以使用快排的思路，在 O(n) 的时间复杂度内完成求解。

/**
 * 快速排序 partition 操作查找
 * 时间复杂度: O(N)
 * 空间复杂度: O(logN)
 */
class Solution {
    public int findKthLargest(int[] nums, int k) {
        return partition(nums, k, 0, nums.length - 1);
    }

    /**
     * partition 操作在 nums[l...r] 中查找第 k 大的元素
     * 每次 partition 后比较 k 和标的 pivot 的下标大小，决定下一次 partition 的范围。
     */
    private int partition(int[] nums, int k, int l, int r) {
        // 选取随机标的
        swap(nums, l, (int) (Math.random() * (r - l + 1) + l));
        int pivot = nums[l];

        int p = l;
        // 进行 partition 操作，将大于 pivot 的元素移到 [l, r] 区间左边
        for (int i = l; i <= r; i++) {
            if (nums[i] > pivot)
                swap(nums, i, ++p);
        }
        swap(nums, l, p);

        // 比较 pivot 的索引 p 和 k 的大小
        if (p + 1 == k) {
            // 如果 p+1 == k，那么 nums[p] 就是第 k 大的元素
            return nums[p];
        } else if (p + 1 > k) {
            // 第 k 大的元素在 nums[p] 左边
            return partition(nums, k, l, p - 1);
        } else {
            // 第 k 大的元素在 nums[p] 右边
            return partition(nums, k, p + 1, r);
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# 指针对撞（两数之和 II - 输入有序数组）

# 问题描述

167. 两数之和 II - 输入有序数组 (opens new window)简单

给定一个已按照 升序排列 的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。

函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ，所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。

你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
1
2
3

这个问题的暴力解法是直接双重循环遍历两个数组，找到所有的数据对，看他们的和是否等于 target。

# 分析实现

  1. 这个问题的暴力解法是直接双重循环遍历两个数组，找到所有的数据对，看他们的和是否等于 target。

    /**
 * 暴力枚举法
 * 时间复杂度 O(n^2)
 * 时间复杂度 O(1)
 */
class Solution {
    public int[] solution1(int[] numbers, int target) {
        for (int i = 0; i < numbers.length - 2; i++) {
            for (int j = i + 1; j < numbers.length - 1; j++) {
                if (numbers[i] + numbers[j] == target) {
                    return new int[]{i, j};
                }
            }
        }
        throw new IllegalStateException("The input has no solution");
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17

  2. 线性遍历 + 二分搜索。

    首先线性遍历数组 nums[0...n-1]，遍历到 nums[i] 的时候，如果数组里有一个数 x 满足 x + nums[i] = target，就能满足题目条件。在剩下的 nums[i+1...n-1] 区间内进行二分搜索，搜索数值等于 target - nums[i] 的元素即可。

    image-20210829113551990

    /**
 * 线性遍历 + 二分查找
 * 时间复杂度 O(nlogn)
 * 时间复杂度 O(1)
 */
class Solution {
    public int[] solution2(int[] numbers, int target) {
        for (int i = 0; i < numbers.length - 1; i++) {
            int j = binarySearch(numbers, i + 1, numbers.length - 1, target - numbers[i]);
            if (j != -1) {
                return new int[]{i + 1, j + 1};
            }
        }
        throw new IllegalStateException("The input has no solution");
    }

    // 二分搜索
    private int binarySearch(int[] numbers, int l, int r, int target) {
        while (l <= r) {
            int mid = (r - l) / 2 + l;
            if (numbers[mid] == target) {
                return mid;
            } else if (numbers[mid] < target) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return -1;
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31

  3. 指针对撞

    image-20210829113841119

    初始指针 i 指向 0 元素，j 指向 n-1 元素，判断 nums[i] + nums[j] 和 target 的大小关系

    • nums[i] + nums[j] == target：正好得到结果，返回 [i, j] 即可
    • nums[i] + nums[j] < target：两个元素和小了，需要大一点，i 向右移动一位再试试
    • nums[i] + nums[j] == target：两个元素和大了，需要小一点，j 向左移动一位再试试

    因为题目肯定有解，所以肯定能在 i < j 的前提下找到结果。

    /**
 * 双端遍历，指针对撞
 * 时间复杂度 O(n)
 * 时间复杂度 O(1)
 */
class Solution {
    public static int[] solution3(int[] numbers, int target) {
        int i = 0, j = numbers.length - 1;
        while (i < j) {
            int sum = numbers[i] + numbers[j];
            if (sum == target) {
                return new int[]{i + 1, j + 1};
            } else if (sum < target) {
                i++;
            } else {
                j--;
            }
        }
        throw new IllegalStateException("The input has no solution");
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21

# 相关问题

下面提供更多指针对撞的相关问题。

125. 验证回文串 (opens new window)简单

给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。

**说明：**本题中，我们将空字符串定义为有效的回文串。

输入: "A man, a plan, a canal: Panama"
输出: true
解释："amanaplanacanalpanama" 是回文串
1
2
3

这里要注意只考虑数字和字符，无效的字符不参与比较。

/**
 * 双指针对撞
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    public boolean isPalindrome(String s) {
        s = s.toLowerCase();
        int l = 0, r = s.length() - 1;

        while (l < r) {
            // 跳过首尾的无效字符
            while (l < r && !isLetter(s.charAt(l)))
                l++;
            while (r > l && !isLetter(s.charAt(r)))
                r--;

            if (s.charAt(l) != s.charAt(r)) {
                return false;
            } else {
                l++;
                r--;
            }
        }
        return true;
    }

    // 辅助方法，验证是不是一个有效字符
    private boolean isLetter(char x) {
        return (x >= 'a' && x <= 'z') || (x >= 'A' && x <= 'Z') || (x >= '0' && x <= '9');
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

344. 反转字符串 (opens new window)简单

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

/**
 * 双指针
 * 时间复杂度：O(N)
 * 空间复杂度：O(1)
 */
class Solution {
    public void reverseString(char[] s) {
        if (s.length == 0) {
            return;
        }
        
        int i = 0, j = s.length - 1;
        while (i < j) {
            char temp = s[i];
            s[i] = s[j];
            s[j] = temp;
            i++;
            j--;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

345. 反转字符串中的元音字母 (opens new window)简单

给你一个字符串 s ，仅反转字符串中的所有元音字母，并返回结果字符串。

元音字母包括 'a'、'e'、'i'、'o'、'u'，且可能以大小写两种形式出现。

/**
 * 双指针对撞
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    public String reverseVowels(String s) {
        char[] chars = s.toCharArray();
        int l = 0, r = chars.length - 1;
        while (l < r) {
            while (l < r && isNotVowel(chars[l]))
                l++;
            while (l < r && isNotVowel(chars[r]))
                r--;

            char temp = chars[l];
            chars[l++] = chars[r];
            chars[r--] = temp;
        }
        return new String(chars);
    }

    private boolean isNotVowel(char x) {
        return (x != 'a') && (x != 'e') && (x != 'i') && (x != 'o') && (x != 'u')
                && (x != 'A') && (x != 'E') && (x != 'I') && (x != 'O') && (x != 'U');
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

11. 盛最多水的容器 (opens new window)中等

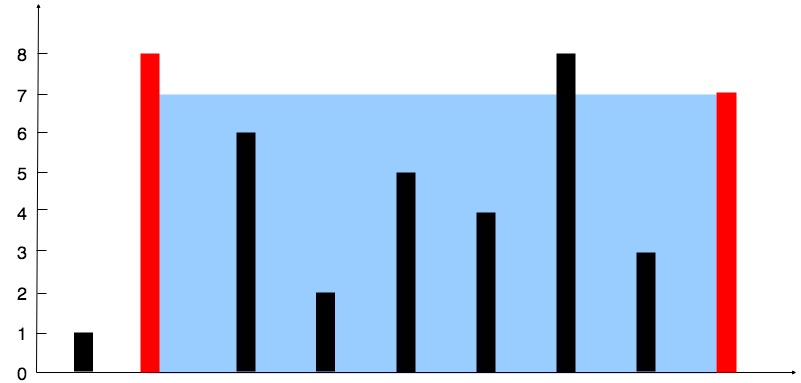
给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

/**
 * 双指针对撞
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    public int maxArea(int[] height) {
        int l = 0, r = height.length - 1;
        int area = 0;
        while (l < r) {
            area = Math.max(area, getArea(height, l, r));
            if (height[l] < height[r]) {
                l++;
            } else {
                r--;
            }
        }
        return area;
    }
    
    // 求容积
    private int getArea(int[] height, int l, int r) {
        return (r - l) * Math.min(height[l], height[r]);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 滑动窗口（长度最小的子数组 ）

# 问题描述

上一节介绍的 对撞指针 是一种双索引技术（Two Pointer），也就是使用两个索引，定义清楚它们的含义，然后使用一一定的规则移动它们。还有一类非常常见的双索引技术，就是 滑动窗口，即两个索引表示的是一个窗口，让这个窗口不停的滑动，来这个数组中游走，来找到我们希望求得的解。

209. 长度最小的子数组 (opens new window)中等

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
1
2
3

# 分析实现

  1. 暴力解法

    遍历所有的连续子数组 [l...r]，计算子数组元素的和 sum，验证 sum > s，同时统计其中最短的长度。时间复杂度是 O(n^3)。

    /**
 * 暴力解法
 * 时间复杂度: O(n^3)
 * 空间复杂度: O(1)
 */
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int res = nums.length + 1;  // 初始一个最数组长度还大的值，表示符合条件的子数组
        for (int l = 0; l < nums.length; l++) {      // 子数组左边界 O(n)
            for (int r = l; r < nums.length; r++) {  // 子数组右边界 O(n)
                int sum = 0;
                for (int i = l; i <= r; i++) {       // 求子数组和 O(n)
                    sum += nums[i];
                }
                if (sum >= target) {
                    res = Math.min(res, r - l + 1);
                }
            }
        }
        
        return res == nums.length + 1 ? 0 : res;  // 判断有没有找到符合条件的子数组
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23

  2. 暴力解法优化

    /**
 * 暴力解法优化
 * 时间复杂度: O(n^2)
 * 空间复杂度: O(1)
 */
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        // sums[i] 表示 nums[0...i-1] 子数组元素的和
        int[] sums = new int[nums.length];
        sums[0] = nums[0];
        for(int i = 1; i < nums.length; i++) {
            sums[i] = sums[i - 1] + nums[i];
        }
        
        int res = nums.length + 1;  // 初始一个最数组长度还大的值，表示符合条件的子数组
        for (int l = 0; l < nums.length; l++) {      // 子数组左边界 O(n)
            for (int r = l; r < nums.length; r++) {  // 子数组右边界 O(n)
                // 直接使用 sums 快速求得 nums[l...r] 的元素和，避免第三层循环
                if (sums[r] - sums[l - 1] >= target) {
                    res = Math.min(res, r - l + 1);
                }
            }
        }
        
        return res == nums.length + 1 ? 0 : res;  // 判断有没有找到符合条件的子数组
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27

  3. 滑动窗口

    定义窗口 [l...r]，如果窗口元素和 sum < target，就让 r 右移，直到 sum >= target，并统计此时窗口长度 size；然后尝试将 l 右移缩小窗口，如果还满足 sum >= target，再次统计 size；直到 sum 值不够了，就再将 r 右移，重复上面操作，直到数组末尾。此时统计的最小的 size 就是问题的结果。

    /**
 * 滑动窗口解法
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int l = 0, r = -1;          // 滑动窗口为 nums[l...r]
        int sum = 0;                // 连续子数组和，即滑动窗口内元素和
        int res = nums.length + 1;  // 连续子数组长度，即滑动窗口元素个数

        while (l < nums.length) {
            if (r + 1 < nums.length && sum < target) {
                // sum 不够且右边界没越界，添加一个元素到窗口中，右边界向右滑
                r++;
                sum += nums[r];
            } else {
                // sum 够了，尝试从左边界拿掉一个元素，左边界右滑
                sum -= nums[l];
                l++;
            }

            // 移动后再统计 sum 够不够，如果够则统计 res
            if (sum >= target) {
                res = Math.min(res, r - l + 1);
            }
        }

        return res > nums.length ? 0 : res;
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31

# 在滑动窗口中做记录（无重复字符的最长子串）

# 问题描述

3. 无重复字符的最长子串 (opens new window)中等

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。s 由英文字母、数字、符号和空格组成。

- "abcabcbb"，结果为 "abc"，返回 3
- "bbbbb"，结果为 "b"，返回 1
1
2

题目中规定字符串 s 由英文字母、数字、符号和空格组成，即可以用 ASCII 码完全表示。

# 分析实现

  1. 暴力解法

    遍历所有的连续子数组 [l...r]，判断子数组内是否有重复元素，涉及到三重循环，时间复杂度 O(n^3)。实现略。

  2. 滑动窗口

    跟上一节长度最小的子数组问题一样，使用双索引维护一个滑动窗口。这里判断窗口内是否有重复元素，不适用遍历的方式，而是用一个 int[128] arr 的数组完全覆盖 ASCII 码的所有字符，用 arr[c] 的值为 1 还是 0，判断窗口内是否有字符 c。

    /**
 * 滑动窗口
 * 时间复杂度: O(n)
 * 空间复杂度: O(1)
 */
class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 定义窗口边界和长度
        int l = 0, r = -1;
        int maxLen = 0;
        // arr[i] == true 表示 (char) i 在窗口里存在，也可以用哈希表
        boolean[] arr = new boolean[128];
        
        while (l < s.length()) {
            if (r + 1 < s.length() && !arr[s.charAt(r + 1)]) {
                r++;
                arr[s.charAt(r)] = true;
            } else {
                arr[s.charAt(l)] = false;
                l++;
            }
            maxLen = Math.max(maxLen, r - l + 1);
        }

        return maxLen;
    }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27

# 相关问题

438. 找到字符串中所有字母异位词 (opens new window)中等

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指字母相同，但排列不同的字符串。

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
1
2
3
4
5
输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
1
2
3
4
5
6

本题也是典型的滑动窗口，和之前的滑动窗口问题不同的是，这里的滑动窗口长度是固定的，等于字符串 p 的长度。只要一开始规定一个长度等于 p.length() 的窗口 s[l, r]，一直往右边滑动，每次都判断是否是 p 的异位词即可。

/**
 * 滑动窗口
 * 时间复杂度: O(len(s) * len(p))  其中 len(s) 表示窗口滑动，len(p) 表示判断是不是异位词
 * 空间复杂度: O(len(p))  其中开辟两个 len(p) 的数组，对比是不是异位词
 */
class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        List<Integer> resList = new ArrayList<>();
        if (s.length() < p.length()) return resList;

        int[] targetArr = new int[26];  // 存放字符串 p 的字母情况
        int[] subArr = new int[26];     // 存放字符串 s 子串的字母情况
        for (int i = 0; i < p.length(); i++) {
            // 记录 p 字符情况
            targetArr[p.charAt(i) - 'a']++;
            // 记录 s 第一个子串字母情况，子串长度同 p
            subArr[s.charAt(i) - 'a']++;
        }

        // 定义滑动窗口边界，长度固定
        int l = 0, r = p.length() - 1;
        while (true) {
            // 如果子串和 p 元素情况相同，找到了符合的子串
            if (isSameArr(targetArr, subArr)) 
                resList.add(l);
            // 滑倒最右边了结束循环
            if (r + 1 == s.length()) 
                break;

            // 窗口右滑一位，更新窗口内元素情况
            subArr[s.charAt(l) - 'a']--;
            subArr[s.charAt(r + 1) - 'a']++;
            l++;
            r++;
        }

        return resList;
    }

    /**
     * 判断两个等长 int 数组各元素是否相同，本题中判断异位词的方法
     */
    private boolean isSameArr(int[] arr1, int[] arr2) {
        for (int i = 0; i < arr1.length; i++) {
            if (arr1[i] != arr2[i]) return false;
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

76. 最小覆盖子串 (opens new window)困难

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。

s 和 t 由英文字母组成。

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
1
2

同样的，滑动窗口，移动右边界直到包含 t 中所有字符，然后尝试移动左边界看看是否还包含，如果不包含了再移动右边界，期间统计最小包含子串的长度和起始索引。

class Solution {
    public String minWindow(String s, String t) {
        if (s.length() < t.length()) return "";

        int[] targetArr = new int['z' - 'A' + 1];   // 存放字符串 p 的字母情况
        int[] subArr = new int['z' - 'A' + 1];      // 存放字符串 s 子串的字母情况
        // 记录 t 和 s 的第一个等长子串的情况
        for (int i = 0; i < t.length(); i++) {
            targetArr[t.charAt(i) - 'A']++;
            subArr[s.charAt(i) - 'A']++;
        }

        int l = 0, r = t.length() - 1;              // 窗口边界
        int index = -1, minLen = s.length() + 1;    // 保存最短子串的起始索引和长度
        while (true) {
            if (containAll(subArr, targetArr)) {  // 子串覆盖了目标串
                // 如果当前窗口长度小于最小长度，重新维护 index 和 minLen
                int currentLen = r - l + 1;
                if (currentLen < minLen) {
                    index = l;
                    minLen = currentLen;
                }
                // 尝试取出左侧元素，即左边界右滑
                subArr[s.charAt(l) - 'A']--;
                l++;
            } else {  // 子串覆盖了目标串，不越界的情况下右边界右滑
                if (++r == s.length()) break;
                subArr[s.charAt(r) - 'A']++;
            } 
        }

        return index == -1 ? "" : s.substring(index, index + minLen);
    }

    /**
     * 用于判断子串是否包含目标串所有字符的方法
     */
    private boolean containAll(int[] subArr, int[] targetArr) {
        for (int i = 0; i < targetArr.length; i++) {
            if (subArr[i] < targetArr[i]) return false;
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
编辑 (opens new window)
上次更新: 2023/06/04, 12:34:19
01-复杂度分析
03-查找表问题

← 03-查找表问题→

最近更新
01
第01章-RabbitMQ导学
02-10
02
第02章-入门RabbitMQ核心概念
02-10
03
第03章-RabbitMQ高级特性
02-10
更多文章>
Theme by Vdoing | Copyright © 2020-2023 CodeAshen | MIT License