 03-查找表问题
03-查找表问题
本章我们来关注查找问题,通常说到查找问题有两类:
查找有无
如判断元素 a 是否存在,通常使用
set,集合查找对应关系(键值对应)
如元素 a 出现了几次,通常使用
map,字典
# Set 的使用(两个数组的交集)
349. 两个数组的交集 (opens new window)简单
给定两个数组,编写一个函数来计算它们的交集。(重复元素只统计一次)
非常简单的一个问题,只需要将 nums1 中所有的元素放到一个 set 中,再遍历 nums2,看元素是否在 set 中,如果在就加到另一个存放结果的 set 中,最后返回结果 set 中的所有元素即可。
/**
* 使用 set 解决
* 时间复杂度: O(m+n)
* 空间复杂度: O(m+n)
*/
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
// 记录 nums1 中所有元素
HashSet<Integer> recordSet = new HashSet<>();
for (int item : nums1) {
recordSet.add(item);
}
// 存放所有交集的 set
HashSet<Integer> resultSet = new HashSet<>();
for (int item : nums2) {
if (recordSet.contains(item)) {
resultSet.add(item);
}
}
// 返回的是数组,转换一下即可
int[] arr = new int[resultSet.size()];
int index = 0;
for (Integer resultItem : resultSet) {
arr[index++] = resultItem;
}
return arr;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# map 的使用(两个数组的交集 II)
350. 两个数组的交集 II (opens new window)简单
给定两个数组,编写一个函数来计算它们的交集。(重复元素只统计多次)
输入:nums1 = [1,2,2,1], nums2 = [2,2] 输出:[2,2]1
2
因为要判断频次,所以使用 map。
/**
* 使用 map 解决
* 时间复杂度: O(nlogn) 其中 n 体现在元素数量上,logn 体现在 TreeMap 的操作上;使用 HashMap 就是 O(n)
* 空间复杂度: O(n)
*/
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
// HashMap 记录 nums1 元素和频次
HashMap<Integer, Integer> recordMap = new HashMap<>();
for (int item : nums1) {
recordMap.put(item, recordMap.getOrDefault(item, 0) + 1);
}
// 遍历 nums2 找出 map 中有的元素,加到 list中,同时减少 map 中元素频次
ArrayList<Integer> list = new ArrayList<>();
for (int item : nums2) {
if (recordMap.containsKey(item) && recordMap.get(item) > 0) {
list.add(item);
recordMap.put(item, recordMap.get(item) - 1);
}
}
// 返回值转换
int[] arr = new int[list.size()];
int index = 0;
for (Integer resultItem : list) {
arr[index++] = resultItem;
}
return arr;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
思考题:对于上面两个交集问题,如果给出的数组是有序的,是否可以根据有序的特性想到更优性能的方法呢?
# set 和 map 不同底层实现的区别
# 不同数据结构的时间复杂度
set 和 map 常见操作的时间复杂度是多少呢?set 和 map 可以有不同的底层实现,set 可以看作 value 为空的 map,实际上 Java 中的 set 确实也是使用 map 实现的,所以相同底层实现的 set 和 map 时间复杂度相同。
基于不同的底层时间 set 和 map 的实际按复杂度如下图所示。
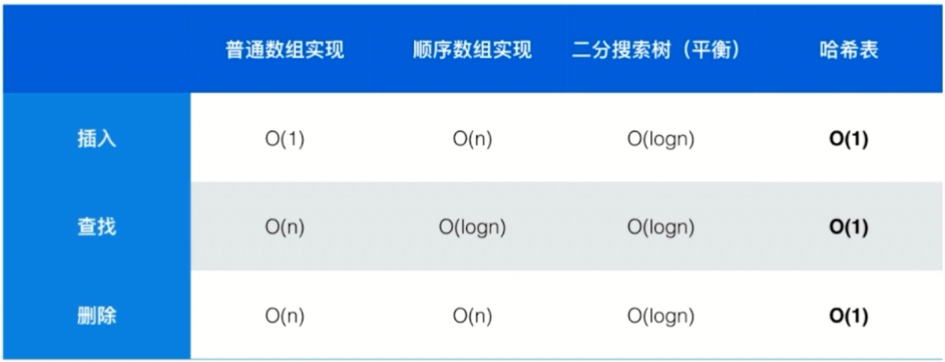
因为 set 是基于 map 的,我们这里就讨论 map 好了。map 的经典底层实现就是二分搜索树(Java中为红黑树)和哈希表,其中哈希表实现的操作时间复杂度都是 O(1) 的,性能非常优秀,但是有一个缺点就是失去了元素的顺序性(这里的顺序是元素大小的顺序,不是插入顺序),而二分搜索树的实现可以保持元素的顺序性,从而快速回答以下问题:
- 数据集中的最大值和最小值
- 某个元素的前驱和后继
- 某个元素的 floor 和 ceil
- 某个元素的排位 rank
- 选择某个排位的元素 select
所以没有以上类似要求的时候直接用哈希表的实现,否则用二分搜索树的实现。
# 更多查找问题
242. 有效的字母异位词 (opens new window)简单
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
哈希表记录字母频次
/** * 哈希表记录字母频次 * 时间复杂度: O(n) * 空间复杂度: O(S) 其中 S 为字符集大小,此处 S=26。 */ class Solution { public boolean isAnagram(String s, String t) { if (s.length() != t.length()) { return false; } // 记录字符串 s 的字母频次 HashMap<Character, Integer> recordMap = new HashMap<>(); for (int i = 0; i < s.length(); i++) { char ch = s.charAt(i); recordMap.put(ch, recordMap.getOrDefault(ch, 0) + 1); } // 遍历字符串 t,判断是否在 map 中 for (int i = 0; i < t.length(); i++) { char ch = t.charAt(i); if (!recordMap.containsKey(ch) || recordMap.get(ch) == 0) { return false; // 如果没有,直接返回 false } else { recordMap.put(ch, recordMap.getOrDefault(ch, 0) - 1); // 如果有,扣掉一次频次 } } return true; // 遍历结束没返回 false,则是字母异位词 } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30数组记录字母频次
数组代替方法一的 map,实际提交到 leetcode 性能更好,省略了 map 里的复杂操作
/** * 数组记录字母频次 * 时间复杂度: O(n) * 空间复杂度: O(S) 其中 S 为字符集大小,此处 S=26。 */ class Solution { public boolean isAnagram(String s, String t) { if (s.length() != t.length()) return false; // 记录 s 和 t 的字母频次关系 int[] record = new int[26]; for (int i = 0; i < s.length(); i++) { record[s.charAt(i) - 'a']++; // s 中有,对应字母频次 +1 record[t.charAt(i) - 'a']--; // t 中有,对用字母频次 -1 } // 对比频次,如果最后每个字母频次都是 0,则为异位词 for (int i : record) { if (i != 0) return false; } return true; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24排序后对比
/** * 排序对比 * 时间复杂度: O(nlogn) * 空间复杂度: O(logn) */ class Solution { public boolean isAnagram(String s, String t) { if (s.length() != t.length()) { return false; } char[] str1 = s.toCharArray(); char[] str2 = t.toCharArray(); Arrays.sort(str1); Arrays.sort(str2); return Arrays.equals(str1, str2); } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 true ;不是,则返回 false 。
输入:19 输出:true 解释: 1^2 + 9^2 = 82 8^2 + 2^2 = 68 6^2 + 8^2 = 100 1^2 + 0^2 + 0^2 = 1 --- 快乐数1
2
3
4
5
6
7
题目提示我们了,如果不是快乐数,它的各数位平方和将循环下去,只需要一直求平方和,放到 set 中,期间如果遇到了平方和为 1,返回 true;如果遇到了和 set 中重复的数,出现循环了,返回 false。
class Solution {
public boolean isHappy(int n) {
HashSet<Integer> set = new HashSet<>();
while (true) {
n = getSum(n);
if (n == 1) {
return true; // 出现 1,返回 true
} else if (set.contains(n)) {
return false; // 出现循环,返回 false
} else {
set.add(n); // 平方和结果加到 set 中
}
}
}
// 计算数字 a 每个数位上的数字的平方和
public int getSum(int a) {
int sum = 0;
while (a > 0) {
sum += (a % 10) * (a % 10);
a /= 10;
}
return sum;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
290. 单词规律 (opens new window)简单
给定一种规律 pattern 和一个字符串 str ,判断 str 是否遵循相同的规律。
这里的 遵循 指完全匹配,例如, pattern 里的每个字母和字符串 str 中的每个非空单词之间存在着双向连接的对应规律。
输入: pattern = "abba", str = "dog cat cat dog" 输出: true1
2
思路:首先肯定是 str 按照空格切分成字符串数组 arr,arr 和 pattern 的长度必须相等为 n;进行 n 次循环,同时遍历 pattern 和 arr,简历 pattern[i] 和 arr[i] 的映射关系,放到 map 里面,后续遇到相同的 pattern 判断是不是那个对那个的字符串。
需要注意的是 patterm = "abc", str = "dog dog dog" 这种 key 不重复但是 value 重复的情况,所以对 value 是否出现过也要判断,用一个 set 存放出现过的 value。
/**
* map + set 解法
*/
class Solution {
public boolean wordPattern(String pattern, String s) {
String[] arr = s.split(" ");
if (arr.length != pattern.length()) {
return false;
}
// map 统计每个 pattern 中字母对应 s 中的单词
HashMap<Character, String> map = new HashMap<>();
// set 统计 s 中已经出现的单词(map 中的 value)
HashSet<String> set = new HashSet<>();
for (int i = 0; i < arr.length; i++) {
char ch = pattern.charAt(i); // pattern[i] 的字符
// 判断是否有映射关系的 key
if (map.containsKey(ch)) {
// 1. 如果有映射关系,判断 value 是否匹配,不匹配就返回 false
if (!arr[i].equals(map.get(ch))) {
return false;
}
} else {
// 2. 如果没有映射关系 key,不要直接建立映射关系,先判断 value 是否出现过
if (set.contains(arr[i])) {
// 2.1 如果value 出现过,说明有 key 不同 value 相同的情况,返回 false
return false;
} else {
// 2.2 如果 value 没出现过,建立新的映射关系,并记录 value
map.put(ch, arr[i]);
set.add(arr[i]);
}
}
}
return true;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
205. 同构字符串 (opens new window)简单
给定两个字符串 s 和 t,判断它们是否是同构的。
如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。
每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序。不同字符不能映射到同一个字符上,相同字符只能映射到同一个字符上,字符可以映射到自己本身。
输入:s = "egg", t = "add" 输出:true1
2
本题和上一题非常类似,几乎一样。
map + set
/** * map + set 解法 */ class Solution { public boolean isIsomorphic(String s, String t) { // s -> t 的字母映射 HashMap<Character, Character> map = new HashMap<>(); // 记录遍历过程中 t 中出现过的字母(映射关系中的 value) HashSet<Character> set = new HashSet<>(); for (int i = 0; i < s.length(); i++) { char keyChar = s.charAt(i); char valueChar = t.charAt(i); // 判断是否有映射关系的 key if (map.containsKey(keyChar)) { // 1. 如果有映射关系,判断 value 是否匹配,不匹配就返回 false if (map.get(keyChar) != valueChar) { return false; } } else { // 2. 如果没有映射关系 key,不要直接建立映射关系,先判断 value 是否出现过 if (set.contains(valueChar)) { // 2.1 如果value 出现过,说明有 key 不同 value 相同的情况,返回 false return false; } else { // 2.2 如果 value 没出现过,建立新的映射关系,并记录 value map.put(keyChar, valueChar); set.add(valueChar); } } } return true; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34数组 + set
数组代替方法一的 map,实际提交到 leetcode 性能更好,省略了 map 里的复杂操作
class Solution { public boolean isIsomorphic(String s, String t) { int[] mapArr = new int[128]; HashSet<Object> set = new HashSet<>(); for (int i = 0; i < s.length(); i++) { if (mapArr[s.charAt(i)] == 0) { if (set.contains(t.charAt(i))) { return false; } else { mapArr[s.charAt(i)] = t.charAt(i); set.add(t.charAt(i)); } } else { if (mapArr[s.charAt(i)] != t.charAt(i)) { return false; } } } return true; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
451. 根据字符出现频率排序 (opens new window)中等
给定一个字符串,请将字符串里的字符按照出现的频率降序排列。
/**
* map + 优先队列
*/
class Solution {
public String frequencySort(String s) {
// map 记录字母频次
HashMap<Character, Integer> freqMap = new HashMap<>();
for (int i = 0; i < s.length(); i++) {
freqMap.put(s.charAt(i), freqMap.getOrDefault(s.charAt(i), 0) + 1);
}
// 优先队列,存放 Map.Entry,按照 value 频次降序排列
PriorityQueue<Map.Entry> queue = new PriorityQueue<>(freqMap.size(), Comparator.comparingInt(o -> - (int) o.getValue()));
queue.addAll(freqMap.entrySet());
char[] chars = new char[s.length()];
int index = 0;
// 按照优先队列里的排序逐个拿出来,放入 value 个 key 就好了
while (!queue.isEmpty()) {
Map.Entry entry = queue.poll();
int freq = (int) entry.getValue();
for (Integer i = 0; i < freq; i++) {
chars[index++] = (char) entry.getKey();
}
}
return new String(chars);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 使用查找表的经典问题(两数之和)
# 题目分析
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target 的那两个整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。
首先暴力解法是遍历所有的数据对,看数据对的和是否是 target,时间复杂度是 O(n^2),显然超时。
我们可以使用查找表,将所有的元素放入查找表,之后对于每一个元素 a,查找 target - a 是否存在。这里选择 Map,key 为 元素值,value 为索引 i,这样时间复杂度为 O(n)。
但是我们要注意,可以直接把所有的 nums[i] -> i 的映射放到 map 里面,然后遍历数组吗?其实这样是有问题的,比如 nums 中有两个 50,而 target=100,此时返回值就是这两个 50 的索引。但是如果一次把所有的映射放到 map 里,后一个 50 的索引就会覆盖前一个 50 的索引,导致遍历过程中取不到这两个索引。
下面我们分析如果解决这个问题,我们完全可以不一次性将所有的元素放入查找表中。当我们遍历整个数组的过程中,当遍历到到元素 v 的时候,我们完全可以之查找 v 前面的元素,看这里面是否有 target - v 这个元素。也就是说我们之将 v 前面的元素放入查找表中,着这种时候如果 v 前面有元素和 v 相等,那此时 v 还没有覆盖前面相等的元素,此时如果查找成功就找到了解;如果查找失败,就将 v 放入查找表,继续遍历下一个元素。这种情况即使覆盖率前面的 v 也不影响现在的 v,因为查找过程中已经证明了 target != 2*v 了,此时只需要查找表中有一个 v 元素就够了。

/**
* 哈希表
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
class Solution {
public int[] twoSum(int[] nums, int target) {
// k: nums 中元素, v: 元素对应的索引
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
if (map.containsKey(target - nums[i])) {
// 如果前面的查找表中有 target - nums[i],直接返回
return new int[]{i, map.get(target - nums[i])};
} else {
// 如果没有有 target - nums[i],将 nums[i] 放入查找表
map.put(nums[i], i);
}
}
throw new IllegalArgumentException("No result");
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 相关问题
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]]1
2
排序 + 指针对撞。难点在不重复的三元组,很容易想到使返回的三元组有序比较容易去重。而实现不重复的关键在于双指针的选取,对于满足条件的有序三元组 (a,b,c),双指针是选 ab 还是 ac 还是 bc 呢?笔者一开始选的是 ac,然后遍历 b,发现比较麻烦,最后选取 bc 作为双指针,遍历 a 会方便很多,具体思路见代码。
/**
* 排序 + 双指针
* 时间复杂度 O(n^2)
*/
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
if (nums == null || nums.length < 3) return res;
Arrays.sort(nums); // O(nlogn)
// 遍历过程中把 i 放在最小的位置上,然后使用 l、r 指针对撞考察 i 右边的元素,
// 得到解后按照 (i,l,r) 的顺序返回,自然是从大到小的,期间进行跳过重复元素操作
for (int i = 0; i < nums.length - 2; i++) {
if (nums[i] > 0) break; // 如果最小的 i 都大于 0,后面都大于 0
if (i > 0 && nums[i] == nums[i - 1]) continue; // 跳过重复的 i
int target = -nums[i]; // 对撞指针需要满足的条件
int l = i + 1, r = nums.length - 1; // 定义双指针
while (l < r) {
if (nums[l] + nums[r] == target) {
res.add(Arrays.asList(nums[i], nums[l], nums[r]));
l++;
r--;
while (l < r && nums[l] == nums[l - 1]) l++; // 跳过重复的 l
while (l < r && nums[r] == nums[r + 1]) r--; // 跳过重复的 r
} else if (nums[l] + nums[r] > target) {
r--;
} else { // nums[l] + nums[r] > target
l++;
}
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
16. 最接近的三数之和 (opens new window)中等
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
输入:nums = [-1,2,1,-4], target = 1 输出:2 解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。1
2
3
本题和上一题十分类似,只不过考察三元组的方式不同,上一题是和等于 0,本题是和接近 target。
/**
* 排序 + 指针对撞
* 时间复杂度: O(n^2)
*/
class Solution {
public int threeSumClosest(int[] nums, int target) {
Arrays.sort(nums); // 排序 nlogn
int res = nums[0] + nums[1] + nums[2]; // 存放结果
// 遍历过程中把 i 放在最小的位置上,然后使用 l、r 指针对撞考察 i 右边的元素,
// 考察 (i,l,r) 三元组的和,看和 target 的接近程度
for (int i = 0; i < nums.length - 2; i++) {
int equalNum = target - nums[i]; // 寻找双指针最接近 equalNum 的情况
int l = i + 1, r = nums.length - 1;
while (l < r) {
res = getClosest(target, res, nums[i] + nums[l] + nums[r]);
if (nums[l] + nums[r] == equalNum) {
return target; // 此时三元组的和正好等于 target
} else if (nums[l] + nums[r] > equalNum) {
r--; // 两数和大于 equal,右边界左移
} else {
l++; // 两数和小于 equal,左边界右移
}
}
}
return res;
}
// 辅助函数,返回 num1 和 num2 中更接近 target 的一个
private int getClosest(int target, int num1, int num2) {
int deltaNum1 = Math.abs(target - num1);
int deltaNum2 = Math.abs(target - num2);
return deltaNum1 < deltaNum2 ? num1 : num2;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
454. 四数相加 II (opens new window)中等
给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组
(i, j, k, l),使得A[i] + B[j] + C[k] + D[l] = 0。为了使问题简单化,所有的 A, B, C, D 具有相同的长度 N,且 0 ≤ N ≤ 500 。所有整数的范围在 -2^28 到 2^28 - 1 之间,最终结果不会超过 2^31 - 1 。
将 A+B 的每一种可能和频次放入查找表:O(n^2),然后再遍历 C+D 的组合过程中,再查找表中搜索互补的元素。
/**
* 分组 + 哈希表
* 时间复杂度: O(n^2)
* 空间复杂度: O(n^2)
*/
class Solution {
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
// 枚举 nums1 和 nums2 的所有组合,将记录组合加和和频次
Map<Integer, Integer> sumMap = new HashMap<>();
for (int item1 : nums1) { // O(n^2)
for (int item2 : nums2) {
int sum = item1 + item2;
sumMap.put(sum, sumMap.getOrDefault(sum, 0) + 1);
}
}
int res = 0;
// 枚举 nums3 和 nums4 的所有组合,在 sumMap 中找 对应的 key
for (int item3 : nums3) { // O(n^2)
for (int item4 : nums4) {
res += sumMap.getOrDefault(-(item3 + item4), 0);
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
49. 字母异位词分组 (opens new window)中等
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母都恰好只用一次。
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"] 输出: [["bat"],["nat","tan"],["ate","eat","tea"]]1
2
本题的关键就在于如何把一组 字母异位词 用一个唯一 key 表示,不同的生成 key 的方式有不同的复杂度。
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<>();
for (String str : strs) {
String key = generateKey(str);
List<String> list = map.getOrDefault(key, new ArrayList<>());
list.add(str);
map.put(key, list);
}
return new ArrayList<>(map.values());
}
// 字符排序后新字符串作为 key
private String generateKey(String str) {
char[] chars = str.toCharArray();
Arrays.sort(chars);
return new String(chars);
}
// 统计字母数量,连起来表示 key
private String generateKey2(String str) {
int[] arr = new int[26];
for (int i = 0; i < str.length(); i++) {
arr[str.charAt(i) - 'a']++;
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < 26; i++) {
if (arr[i] != 0) {
sb.append('a' + i).append(arr[i]);
}
}
return sb.toString();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 灵活选择键值(回旋镖的数量)
# 题目分析
447. 回旋镖的数量 (opens new window)中等
给定平面上 n 对 互不相同 的点 points ,其中 points[i] = [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ,其中 i 和 j 之间的距离和 i 和 k 之间的距离相等(需要考虑元组的顺序)。
返回平面上所有回旋镖的数量。
输入:points = [[0,0],[1,0],[2,0]] 输出:2 解释:两个回旋镖为 [[1,0],[0,0],[2,0]] 和 [[1,0],[2,0],[0,0]]1
2
3
若使用暴力解法,可以枚举所有的三元组,验证其是否满足条件,这样的时间复杂度是 O(n^3),我们进一步思考是否可以在 O(n^2) 的复杂度完成求解。
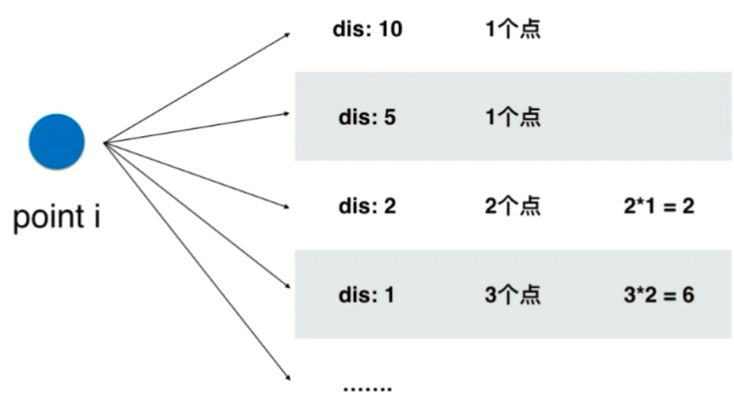
可以发现符合条件的三元组 (i, j, k) 是以 i 为枢纽的,对于每一个点 i,遍历其余点到 i 的距离。根据这样的思路我们可以对每一个点 i 建立一个查找表,key 为其他点到 i 的距离 dis,value 为和 i 距离为 dis 的点的个数。如下图所示,dis=10 和 dis= 5 的点只有 1 个,组不成回旋镖;dis=2 的点有 2 个,从中选出两个点组成飞镖有几种情况呢?是一个选择排列问题,有 2! / (2-2)! = 2 种;dis=1 的点有 3 个,从中选出两个有 3!/ (3-2)! = 6 种。
/**
* 哈希表解法
* 时间复杂度: O(n^2)
* 空间复杂度: O(n),虽然开了 n 个 map,但是每次遍历完,map 空间就释放了
*/
class Solution {
/**
* 遍历到点 i 记录距离频次 map,再遍历 map
* @param points 二维数组,一维索引表示点的个数 n,二维索引只有两个分别表示横纵坐标
* @return 返回回旋镖数量
*/
public int numberOfBoomerangs(int[][] points) {
int res = 0;
for (int i = 0; i < points.length; i++) {
// disCountMap 中存储点 i 到所有其他点的距离出现的频次
Map<Integer, Integer> disCountMap = new HashMap<>(); // 距离-频次 映射
for (int j = 0; j < points.length; j++) {
if (j != i) {
int dis = dis(points[i], points[j]);
disCountMap.put(dis, disCountMap.getOrDefault(dis, 0) + 1);
}
}
// 遍历 disCountMap 找到频次大于 2 的距离,计算可以得到回旋镖的个数
for (Integer count : disCountMap.values()) {
res += count * (count - 1); // 只出现一次也没关系,第二个乘数为 0
}
}
return res;
}
// 计算两个点的距离,用平方表示,不开根号
private int dis(int[] point1, int[] point2) {
return (point1[0] - point2[0]) * (point1[0] - point2[0]) +
(point1[1] - point2[1]) * (point1[1] - point2[1]);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 相关问题
149. 直线上最多的点数 (opens new window)困难
给你一个数组
points,其中points[i] = [xi, yi]表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
/**
* 哈希表统计斜率-频次
*/
class Solution {
public int maxPoints(int[][] points) {
int n = points.length;
if (n <= 2) return n;
int res = 0;
for (int i = 0; i < n; i++) {
HashMap<String, Integer> map = new HashMap<>(); // 斜率-频次 map
for (int j = 0; j < n; j++) {
if (j == i) continue;
String slope = getSlope(points[i], points[j]);
map.put(slope, map.getOrDefault(slope, 0) + 1);
}
for (Integer value : map.values()) {
res = Math.max(res, value + 1); // 要包含 i 点本身,故 +1
}
}
return res;
}
// 求点 p、q 两点的斜率
private String getSlope(int[] p, int[] q) {
int x = p[0] - q[0];
int y = p[1] - q[1];
if (x == 0) {
return "0,1";
} else if (y == 0) {
return "1,0";
} else {
if (y < 0) { // 分子固定正数
x = -x;
y = -y;
}
int gcdXY = gcd(Math.abs(x), Math.abs(y));
x /= gcdXY;
y /= gcdXY;
return x + "," + y;
}
}
// 求最大公约数
private int gcd(int a, int b) {
return b != 0 ? gcd(b, a % b) : a;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 查找表和滑动窗口(存在重复元素 II)
# 题目分析
219. 存在重复元素 II (opens new window)简单
给定一个整数数组和一个整数 k,判断数组中是否存在两个不同的索引 i 和 j,使得 nums[i] = nums[j],并且 i 和 j 的差的 绝对值 至多为 k。
暴力解法:枚举所有的数据对,判断是否满足 nums[i] = nums[j] && Math.abs(i - j) <= k,时间复杂度 O(n^2)。
不过对于问题中两个元素距离不能超过 k 这个条件,很容易想到使用滑动窗口,可以将问题转化为能都在 nums[l...l+k] 的范围内找到两个相同的元素。
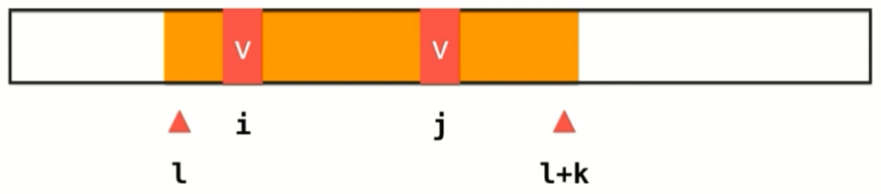
上述区间内没有找到两个相同的元素,则只需要将 l 向前移动一位,然后考察元素 num[l+k+1] 是否在前面的 nums[l+1...l+k] 区间中存在,如果存在就找到了答案直接返回 true,如果不存在,将元素 num[l+k+1] 纳入区间内,然后左边界再 +1,继续考察右边界后面的元素即可。

/**
* set + 滑动窗口
* 时间复杂度: O(n)
* 空间复杂度: O(k)
*/
class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
if (k == 0) return false;
// 存放滑动窗口内的元素
HashSet<Integer> set = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
// 如果窗口元素包含当前遍历到的元素,直接返回 true
if (set.contains(nums[i]))
return true;
// 否则将当前元素加到窗口内容
set.add(nums[i]);
// 如果窗口元素数量超过 k 个,移除窗口左边界的元素
if (set.size() == k + 1)
set.remove(nums[i - k]);
}
return false;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 相关问题
217. 存在重复元素 (opens new window)简单
给定一个整数数组,判断是否存在重复元素。
如果存在一值在数组中出现至少两次,函数返回
true。如果数组中每个元素都不相同,则返回false。
超简单的题,放到 set 里检测就好了,没什么可看的。
class Solution {
public boolean containsDuplicate(int[] nums) {
HashSet<Object> set = new HashSet<>();
for (int item : nums) {
if (set.contains(item))
return true;
set.add(item);
}
return false;
}
}
2
3
4
5
6
7
8
9
10
11
# 二分搜索树底层实现的顺序性(存在重复元素 III)
# 题目分析
220. 存在重复元素 III (opens new window)中等
给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j,使得 abs(nums[i] - nums[j]) <= t ,同时又满足 abs(i - j) <= k 。
如果存在则返回 true,不存在返回 false。
本题我们也可以使用滑动窗口,我们遍历倒窗口外的元素 v,需要在窗口内查找是否有满足条件的元素 x,使得 abs(v-x) <= t,也就是说寻找一个元素 x 满足 v-t <= x <= v+t。

如果我们将窗口内是原有元素放进查找表中,我们剩下的事情就是看有没有某个元素是满足 [v-t, v+t] 要求的,如果我们的查找表有顺序性的话解决起来就非常容易。如果查找表支持 ceil 和 floor 两个操作的话,我们就可以尝试寻找 ceil(v-t),如果 ceil(v-t) <= v+t 那么就可以说查找表内一定有一个元素在 [v-t, v+t] 区间内的。同理如果查找表中有 floor(v+t) >= v-t 也满足条件,两个函数我们选其一即可。
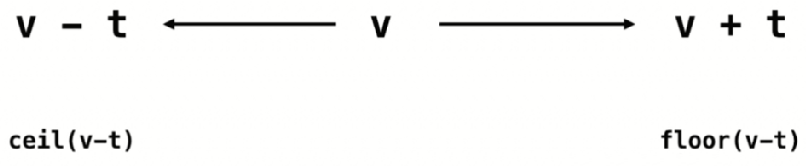
滑动窗口 + TreeSet。使用上面分析的思路
/** * 滑动窗口 + TreeSet * 时间复杂度: 时间复杂度: O(nlogk) * 空间复杂度: O(k) */ class Solution { /** * 滑动窗口 + TreeSet * @param nums 元素数组 * @param k 索引 delta * @param t 元素 delta */ public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) { TreeSet<Long> treeSet = new TreeSet<>(); // 有序查找表,存放滑动窗口内元素 for (int i = 0; i < nums.length; i++) { // 查找表中搜索大于等于 nums[i] - t 的元素 Long ceiling = treeSet.ceiling((long) nums[i] - (long) t); // 如果元素存在且小于等于 nums[i] + t,则存在元素落在 [nums[i]-t, nums[i]+t] 区间内,返回 true if (ceiling != null && ceiling <= (long) nums[i] + (long) t) { return true; } treeSet.add((long) nums[i]); // 没有找到符合的元素,将此元素放入查找表 if (treeSet.size() > k) { // 控制窗口大小 treeSet.remove((long) nums[i - k]); } } return false; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30桶。桶的解法看自 leetcode 官方解释。
class Solution { public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) { int n = nums.length; Map<Long, Long> map = new HashMap<Long, Long>(); long w = (long) t + 1; for (int i = 0; i < n; i++) { long id = getID(nums[i], w); if (map.containsKey(id)) { return true; } if (map.containsKey(id - 1) && Math.abs(nums[i] - map.get(id - 1)) < w) { return true; } if (map.containsKey(id + 1) && Math.abs(nums[i] - map.get(id + 1)) < w) { return true; } map.put(id, (long) nums[i]); if (i >= k) { map.remove(getID(nums[i - k], w)); } } return false; } public long getID(long x, long w) { if (x >= 0) { return x / w; } return (x + 1) / w - 1; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
